Ich blicke mit meinen mystischen Kräften in die Zukunft und sage voraus, dass eine Kartoffel im Schnellkochtopf eher gar wird als in einem normalen Kochtopf!
Zugegeben, die Vorhersage selbst ist recht banal und meine mystischen Kräfte scheinen sich damit nicht gut für weltbewegende Vorhersagen zu eignen.
Aber: Lassen wir einmal die Qualität der Vorhersage beiseite.
Wie können wir solche Vorhersagen überhaupt treffen?
Ein guter Einstieg zur Beantwortung der Frage scheint die Physik zu sein, da unsere Kartoffel-Vorhersage offensichtlich mit bestimmten physikalischen Größen, wie Temperatur und Druck, in Verbindung steht. Weil man in der Physik jedoch weniger mit Schnellkochtöpfen und Kartoffeln hantiert, betrachten wir die physikalische Vorhersage auch aus einer physikalisch-idealisierten Perspektive.
Aus dem Schnellkochtopf, der Kartoffel und dem Wasser wird ein Gefäß mit konstanten Volumen V, welches mit einem bestimmten idealen Gas bei Raumtemperatur gefüllt ist (Abb. 1, links). Wenn wir anschließend den Herd bzw. Bunsenbrenner anmachen und den isochoren thermischen Prozess starten, d.h. bei konstantem Volumen die Temperatur T erhöhen, können wir vorhersagen, dass sich der Druck p des Gases im Gefäß erhöht (Abb. 1, rechts).
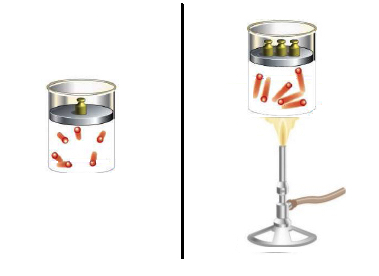
Im ersten Moment scheinen wir unserem Ziel auf diese Weise nicht Näher gekommen zu sein. Vielmehr scheint es, als hätten wir durch die physikalische Idealisierung die Vorhersage nur unnötig kompliziert ausgedrückt.
Jedoch trügt der Schein, denn der deutsche Physiker und Philosoph Heinrich Hertz (1857 – 1894) hat sich mit der Problematik von physikalischen Vorhersagen auseinander gesetzt und eine ganz besondere Methode entwickelt (siehe auch Abb. 2):
„Wir machen uns innere Scheinbilder oder Symbole der äußeren Gegenstände, und zwar machen wir sie von solcher Art, daß die denknotwendigen Folgen der Bilder stets wieder die Bilder seien von den naturnotwendigen Folgen der abgebildeten Gegenstände.“ (Hertz, 1884, S. 1)
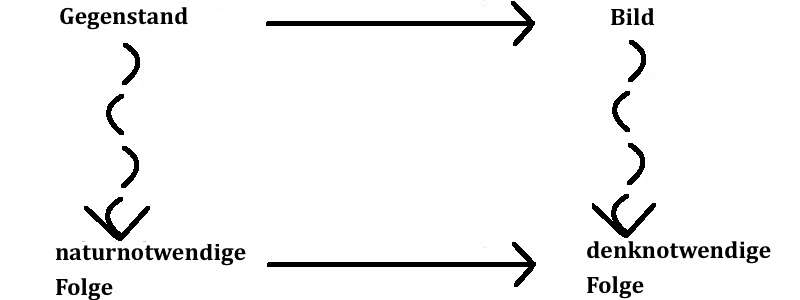
Der Kerngedanke dieser Methode ist, dass das physikalische Untersuchungsobjekt (Gegenstand), wie der isochore thermische Prozess, als Bild aufgefasst wird. Damit ist gemeint, dass nicht mit dem Gegenstand operiert wird, sondern nur mit dem angefertigten Bild. Dabei gilt, dass das Bild keine eins-zu-eins Spiegelung oder Kopie ist, sondern vielmehr den Gegenstand repräsentiert und gewisse Merkmale aufweist. (Vgl. Jammer, 1965)
Zur Veranschaulichung dieser Beziehung kann man sich zwei Gemälde A und B vorstellen. Das Gemäldes A stellt eine naturgetreue Kopie eines Laubbaums dar. Es wurde penibelst darauf geachtet, dass die Farben und die Gestalt des Baumes exakt wiedergegeben wurden.
Das Gemälde B hingegen bildet ausschließlich gewisse Merkmale des Baums ab, wie den Stamm und die Baumkrone. Eigenschaften wie Farbe und Gestalt des Baumes wurden nach den Vorstellungen der/des Künstler(in) gewählt und nicht vom Original kopiert . (Vgl. Schiemann, 2008; Lützen, 2005)
Was die gewissen Merkmale in dem Gemälde B sind, sind in den Bildern der Physik mathematische Systeme von Gleichungen.
Für unser Beispiel des thermischen Prozesses etwa, kann man hier die Zustandsgleichung idealer Gase anführen, in der die physikalischen Größen Druck, Volumen und Temperatur in einer gewissen mathematischen Beziehung gesetzt sind.
Darüber hinaus finden wir die Physikerin und den Physiker, wie die Malerin oder den Maler des Gemäldes B, in der Situation, ihre Vorstellungen mit einfließen zu lassen.
So geht beispielsweise mit dem Bild des Atoms – mit Blick auf die klassische Physik bzw. kinetische Gastheorie – eine runde Gestalt, eine gewisse Härte und Elastizität einher.
Für unseren thermischen Prozess gilt dann, dass das Gefäß mit kleinsten Atomen angefüllt ist, die chaotisch durcheinander wirbeln und aufgrund ihrer Beschaffenheit zu Stoßprozessen fähig sind (s. Abb. 1).
Im Gegensatz zur Kunst, die zwischen den Stylen von Gemälde A und B wählen können, ob die eigenen Vorstellen mit einfließen sollen, ist dieses in der Physik notwendig. Denn das Hinzufügen von physikalischen Vorstellungen „[...] ist eine allgemeine und nothwendige Eigenschaft des menschlichen Verstandes [...]“ (Hertz, 1884, S. 35).
Im Wesentlichen setzt sich ein (physikalisches) Bild eines Gegenstandes demnach aus einem mathematischen System und den notwendigen physikalischen Vorstellungen zusammen.
Wie hilft uns nun dieses Wissen über die Bilder in der Physik bei der Beantwortung der Frage, wie wir physikalische Vorhersagen aufstellen können?
An diesem Punkt treten die denknotwendigen Folgen in Erscheinung (s. Abb. 2).
Vereinfacht gesprochen leiten wir aus dem relevanten mathematischen System von Gleichungen mit Hilfe von mathematischen Operationen bestimmte gültige mathematische Konsequenzen ab. Diese erneut mit physikalischen Vorstellungen behaften Konsequenzen können wir dann als physikalische Vorhersagen interpretieren. Dabei gilt, dass diese Konsequenzen die Bilder der vorhergesagten Gegenstände, d.h. der naturnotwendigen Folgen, sind.
Mit Blick auf unser Beispiel bedeutet dies, dass aus der Zustandsgleichung idealer Gase für ein konstantes Volumen die mathematische Konsequenz abgeleitet werden kann, dass bei einer Erhöhung der Gastemperatur auch der Gasdruck ansteigt. Mit dieser denknotwendigen Folge geht dann auch die Vorstellung einher, dass sich die Atome bei wachsender Temperatur immer schneller bewegen und sich weiter verteilen wollen. Aufgrund des konstanten Volumens ist dieses aber nicht möglich und der Druck erhöht sich. Die proportionale Beziehung zwischen Temperatur und Druck sowie die damit einhergehende physikalische Vorstellung stellen dann das neue Bild des vorhergesagten, neuen Gegenstandes des angeregten isochoren thermischen Prozesses dar.
Was müssen wir also letztendlich auf die Frage antworten, wie wir überhaupt physikalische Vorhersagen treffen können?
So banal eine Vorhersagen auch erscheinen mag, es ist zunächst notwendig, ein Bild des Gegenstandes anzufertigen. Denn erst wenn wir uns ein Bild von diesem gemacht haben, lassen sich anschließend die denknotwendigen Folgen bzw. Vorhersagen von diesem ableiten und wir können in die Zukunft blicken.
Literatur:
Hertz, H.
1894 Die Prinzipien der Mechanik in neuem Zusammenhange dargestellt, hrsg. von P. Lenard, Edition von 1963, Wissenschaftliche Buchgesellschaft, Darmstadt.
Jammer, M.
1965 “Die Entwicklung des Modellbegriffes in den physikalischen Wissenschaften”, Studium Generale, 18, 3, S. 166-173.
Lützen, J.
2005 Mechanistic Images in Geometric Form. Oxford University Press, Oxford
Schiemann, G.
2008 „Verlust der Welt im Bild. Ursprung und Entwicklung des Bildbegriffes bei Hermann von Helmholtz und Heinrich Hertz“, Heinrich Hertz (1857-1894) and the Development of Communication, S. 31–51. Books on Demand, Norderstedt
